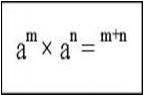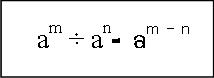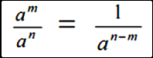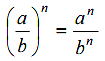เลขยกกำลัง
คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
ตัวอย่าง
25 เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
และ 25 = 2x2x2x2x2 = 32
สมบัติของเลขยกกำลัง
1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก
เช่น 23x 27x 29 = 2 (3 + 7 + 9) = 219
2. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก
กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n
เช่น 412÷ 43=412-3 = 49
กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = n
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a0 = 1
เช่น 67÷ 67 = 67-7 = 60 = 1 หรือถ้า (-7)o = 1
กรณีที่ 3 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n
เช่น  = 1/ 54-9
= 1/ 54-9
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว
 หรือ
หรือ 
เช่น  หรือ
หรือ 
3.สมบัติอื่นๆของเลขยกกำลัง
1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง
 เมื่อ a ≥0 และ m, n เป็นจำนวนเต็ม
เมื่อ a ≥0 และ m, n เป็นจำนวนเต็ม
เช่น 
2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน
 และ
และ 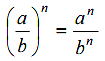 เมื่อ a ≠ 0 , b ≠ 0 และ n เป็นจำนวนเต็ม
เมื่อ a ≠ 0 , b ≠ 0 และ n เป็นจำนวนเต็ม
เช่น 
3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน
 เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1
เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1
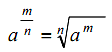 เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2
เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2
การใช้เลขยกกำลังแทนจำนวน
การเขียนจำนวนที่มีค่ามากๆนิยมเขียนแทนได้ด้วยรูป Ax10nเมื่อ 1≤A<10 และ n เป็นจำนวนเต็มบวก เช่น 16,000,000 = 1.6×107 และทำนองเดียวกันการเขียนจำนวนเต็มที่มีค่าน้อยๆก็สามารถเขียนในรูป Ax10n ได้เช่นเดียวกัน แต่ n จะเป็นจำนวนเต็มลบ เช่น 0.000016 = 1.6×10-5
หลักการเปลี่ยนจำนวนให้อยู่ในรูป Ax10n เมื่อ 1≤A<10 และ n เป็นจำนวนเต็มอย่างง่ายๆ คือให้พิจารณาว่าจุดทศนิยมมีการเลื่อนตำแหน่งไปทางซ้ายหรือขวากี่ตำแหน่ง ถ้าเลื่อนไปทางซ้ายเลขชี้กำลังจะเป็นบวก และถ้าเลื่อนไปทางขวาเลขชี้กำลังก็จะเป็นลบ
เช่น 75000.0=7.5×104
0.000075 = 7.5×10-5
หรือกล่าวได้ว่า ถ้าจุดทศนิยมเลื่อนไปทางขวา n ตำแหน่ง เลขชี้กำลังของ 10 จะลดลง n ถ้าจุดทศนิยมเลื่อนไปทางซ้าย n ตำแหน่ง เลขชี้กำลังของ10 จะเพิ่มขึ้น n
สรุป
เลขยกกำลังเป็นการคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) หรือจะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa) อีกทั้งวิธีการคำนวณหาค่าเลขยกกำลังจะขึ้นอยู่กับสมบัติของเลขยกกำลังในแต่ละประเภทด้วย
การบวกเลขยกกำลัง
1.การบวกลบเลขยกกำลังที่มีฐานเหมือนกันและเลขยกกำลังเท่ากัน ให้นำสัมประสิทธิ์ของเลขยกกำลังมาบวกลบกัน
ตัวอย่าง 
2.การบวกลบเลขยกกำลังที่มีฐานเท่ากัน แต่เลขยกกำลังไม่เท่ากันจะนำสัมประสิทธิ์มาบวกลบกันไม่ได้ ต้องทำในรูปของการแยกตัวประกอบ และดึงตัวประกอบร่วมออก
ตัวอย่าง
หมายเหตุ
(-2)4 และ -24 มีค่าไม่เท่ากันเพราะ (-2)4 ฐานคือ (-2)
เลขชี้กำลังคือ 4 อ่านว่าลบสองทั้งหมดยกกำลังสี่มีค่าเท่ากับ 16
-24 ฐานคือ 2 เลขชี้กำลังคือ 4 อ่านว่าลบของสองกำลังสี่มีค่าเท่ากับ -16